flowchart
B[Code body] --> C{Condition}
C -- True --> D[Execute if True]
C -- False --> E[Execute if False]
D & E --> F[Code body]
Conditional execution diagram.
Conditional execution means that some statements are executed only if some condition is true. This can be seen as a forking path in the program flow: Computer executes one branch or the other, depending on the condition.
flowchart
B[Code body] --> C{Condition}
C -- True --> D[Execute if True]
C -- False --> E[Execute if False]
D & E --> F[Code body]
Conditional execution diagram.
The if statement requires a conditional expression (something True or False).
General structure of a conditional statement:
if(<condition>) {
<statements 1>
} else {
<statements 2>
}If the <condition> is true, <statements 1> are executed. Otherwise, <statements 2> are executed.
The value of the last statement in the executed block is returned.
else can be omitted. In that case, when the condition is false, the if-block is skipped.
Suppose the passing grade in a course is 50. If the grade is greater than 50, display the message “Passed”.

grade <- 55
if(grade>50){
"Passed!"
}[1] "Passed!"grade <- 45
if(grade>50){
"Passed!"
}If we have more than one statement inside an if-block, we must use braces to indicate the limits of the block.
The if statement is actually a function, and it returns the value of the last statement in the if-block.
Suppose the following code is inside a bigger program which reads grades in a loop, and counts the students that have passed:
grade <- 40
number_passed <- 0
if (grade>50) {
number_passed <- number_passed + 1
"Passed"
}
number_passed[1] 0If we omit the braces, the code still runs but it gives an incorrect response.
grade <- 40
number_passed <- 0
if (grade>50)
number_passed <- number_passed + 1
"Passed"[1] "Passed"number_passed[1] 0This occurs because, without braces, this code is equivalent to:
grade <- 40
number_passed <- 0
if (grade>50){
number_passed <- number_passed + 1
}
"Passed"
number_passedAs a result, the message "Passed" appears even though the condition is FALSE. However, number_passed is not incremented.
In the example above, the program responds only when the grade is greater than 50.
Suppose we want to get a response for any grade, either “Passed” or “Failed”.
One way:
passed <- function(grade){
if (grade>50) {
retval <- "Passed!"
}
if (grade <= 50) {
retval <- "Failed"
}
retval
}
passed(45)[1] "Failed"Better way: Using the else statement together with if.

grade <- 55
if (grade>50) "Passed!" else "Failed."[1] "Passed!"The if-else statement is actually a function, returning the last statement in the executed block. We can use this feature to capture the output of the if-else and store it in a variable.
grade <- 45
status <- if (grade>50) "Passed" else "Failed"
status[1] "Failed"In the examples above, we have used the > (greater than) operator. There are several such operators for comparing values. Each of these expressions return Boolean (True/False) values.
| operation | meaning |
|---|---|
| a == b | a is equal to b |
| a != b | a is not equal to b |
| a < b | a is less than b |
| a <= b | a is less than or equal to b |
| a > b | a is greater than b |
| a >= b | a is greater than or equal to b |
<= is correct, =< is incorrect.2 < 5[1] TRUE2 >= 5[1] FALSE1 == 2[1] FALSE1 != 2[1] TRUEWhen used with vectors, these operations are applied elementwise, and a Boolean vector is returned.
x <- c(2,3,4)
y <- c(6,1,4)
x >= y[1] FALSE TRUE TRUENote that the if() statement expects a single True/False value as an argument. When it receives a Boolean vector, it uses only the first element to make the comparison.
if (x>=y) "foo" else "bar"Error in if (x >= y) "foo" else "bar": the condition has length > 1If you want to check if the relation holds for every pair of elements in x and y, you should use the all() function.
x <- c(2,3,4)
y <- c(1,0,5)
x>=y[1] TRUE TRUE FALSEall(x>=y)[1] FALSEif(all(x>=y)) "foo" else "bar"[1] "bar"any(x>=y)[1] TRUEif(any(x>=y)) "foo" else "bar"[1] "foo"Floating-point numbers are numbers with a decimal point. They are stored in a special way in computer systems for efficiency and accuracy in calculations. However, this special way causes some errors in representations(truncation error and roundoff error). Numbers that should be mathematically equal can turn out to be nonequal in the computer.
Example:
x <- 10.1 - 10
y <- 0.1
x == y[1] FALSEEven though x and y are mathematically equal, their representations in the computer’s memory are not. For this reason, the equality check returns FALSE
To check the equality of two floating-point numbers, programmers check if their difference is smaller than a threshold:
abs(x-y)<1e-15[1] TRUEThe value 1e-15 is the notation for \(10^{-15}\). It is about the same as the machine precision, which is the error the computer makes when representing a real number.
R has a built-in function all.equal() that checks for almost-equality, within the errors of the machine.
all.equal(x,y)[1] TRUEOften, we need to combine two or more conditions in order to get a more complicated condition. For example
IF (you are younger than 18) AND (you are male)
THEN (you are a boy).
IF (you have heart condition) OR (you are pregnant)
THEN (you should not drink alcohol).
IF (you are older than 18) AND (you are NOT married)
THEN (you can get married).Every logical condition can be expressed by combining AND, OR, and NOT operators.
| operation | meaning |
|---|---|
| a & b | Boolean AND for vectors |
| a | b | Boolean OR for vectors |
| !a | Boolean negation |
| a && b | Boolean AND for scalars |
| a || b | Boolean OR for scalars |
x <- c(T, F, T, F)
y <- c(F, T, T, F)
x & y[1] FALSE FALSE TRUE FALSEx | y[1] TRUE TRUE TRUE FALSE!x[1] FALSE TRUE FALSE TRUEAs seen above, & and | operators can take vector operands, and return a vector of Booleans.
In contrast, && and || operators work with scalars and return only a single Boolean value. If vectors are given to them as operands, they use only the first elements of these vectors.
(1>2) && (3<5)[1] FALSEc(T,F) || c(F,F) # same as T || FError in c(T, F) || c(F, F): 'length = 2' in coercion to 'logical(1)'This distinction exists because if() should take only a single Boolean value for comparison. It would not be correct to use & with if, though it will give us an answer based on the first elements.
x <- c(TRUE, FALSE, TRUE)
y <- c(TRUE, TRUE, FALSE)
if (x && y) "Both True!"Error in x && y: 'length = 3' in coercion to 'logical(1)'if (x & y) "Both TRUE"Error in if (x & y) "Both TRUE": the condition has length > 1ifelse() functionConsider the following task: We have a vector composed of the ages of people.
ages <- c(Ali=16, Fatma=9, Mehmet=65, Elif=41, Zehra=12)
ages Ali Fatma Mehmet Elif Zehra
16 9 65 41 12 Based on this, we want to create a vector with two values: "Child" or "Adult".
Ali Fatma Mehmet Elif Zehra
Child Child Adult Adult Child Using if-else with this vector does not work because it expects a single True/False value.
if(ages<18) "Child" else "Adult"Error in if (ages < 18) "Child" else "Adult": the condition has length > 1To get a vector consisting of desired values, we use the vectorized function ifelse().
First note that ages<18 gives a vector of boolean values:
ages<18 Ali Fatma Mehmet Elif Zehra
TRUE TRUE FALSE FALSE TRUE The following ifelse function takes a boolean vector, returns a new vector with "Child" for true, "Adult" for false:
ifelse(ages<18, "Child","Adult") Ali Fatma Mehmet Elif Zehra
"Child" "Child" "Adult" "Adult" "Child" This could also be done with vector filtering, albeit in a more clumsy way.
temp <- ages # copy ages to new vector
temp[1:length(temp)] <- "Adult" # replace all elements with "Adult"
temp[ages<18] <- "Child" # replace some elements with "Child"
temp Ali Fatma Mehmet Elif Zehra
"Child" "Child" "Adult" "Adult" "Child" Any kind of statements can be put into an if-block, including other if statements. This allows us to make successive decisions. For example, here is a code that prints the level of a grade.
x <- 20
if (x>75) {
"Top"
} else {
if (x>50) {
"Middle"
} else {
if (x>25) {"Low"
} else { "Bottom" }Error in parse(text = input): <text>:10:0: unexpected end of input
8: if (x>25) {"Low"
9: } else { "Bottom" }
^The same structure can also be written in one line, but it would not be very readable.
x <- 25
if (x>75) "Top" else if (x>50) "Middle" else if (x>25) "Low" else "Bottom"[1] "Bottom"Here is a nested if-else structure that determines the region where a given point belongs.
x <- 2
y <- -3
if(x>0) {
if(y>0) {
"upper right"
} else { # y<=0
"lower right"
}
} else { # x<=0
if(y>0) {
"upper left"
} else { # y<=0
"lower left"
}
}[1] "lower right"Another version of the same program:
x <- 5
y <- -3
ypos <- if (y>0) "upper" else "lower"
xpos <- if (x>0) "right" else "left"
cat(ypos,xpos)lower rightAs another example, let us read an integer, and produce a response according to whether it is negative, divisible by two, or divisible by three.
n <- 6
if (n<0) {
"Negative."
} else {
if (n%%2 == 0) {
"Divisible by 2."
} else {
if (n%%3 == 0) {
"Divisible by 3."
} else {
"Nonnegative, not divisible by 2 or 3."
}
}
}[1] "Divisible by 2."Consider the continuous function
\[ f(x) = \begin{cases} x^2 + 2x + 3 & x\lt 0 \\ x+3 & 0\leq x \lt 2 \\ x^2 + 4x -7 & 2\leq x \end{cases}\]
Write a function that takes a single numeric argument x. The function should return the value of the function f(x).
Modify the function so that it takes a vector argument x, and returns a vector consisting of the function values evaluated at each element of the vector x.
Plot the function f (x) for −3 < x < 3.
myfunc <- function(x) {
if(x<0){
return (x^2 + 2*x + 3)
}
else if (x<2){
return (x + 3)
}
else {
return (x^2 + 4*x - 7)
}
}Test the function with values from different regions and verify that they give the correct answer.
myfunc(-1)[1] 2myfunc(1)[1] 4myfunc(3)[1] 14myfunc(c(-1,1,3))Error in if (x < 0) {: the condition has length > 1It is possible to do this with sapply, without modifying the original function definition.
sapply(c(-1,1,3), myfunc)[1] 2 4 14However, if we need a genuinely vectorized function, we can redefine the function using ifelse.
myfunc_vec <- function(x) {
ifelse(x<0, x^2 + 2*x + 3, ifelse(x<2, x+3, x^2 + 4*x - 7))
}myfunc_vec(c(-1,1,3))[1] 2 4 14x <- seq(-3,3,length.out = 101)
plot(x, myfunc_vec(x), type="l")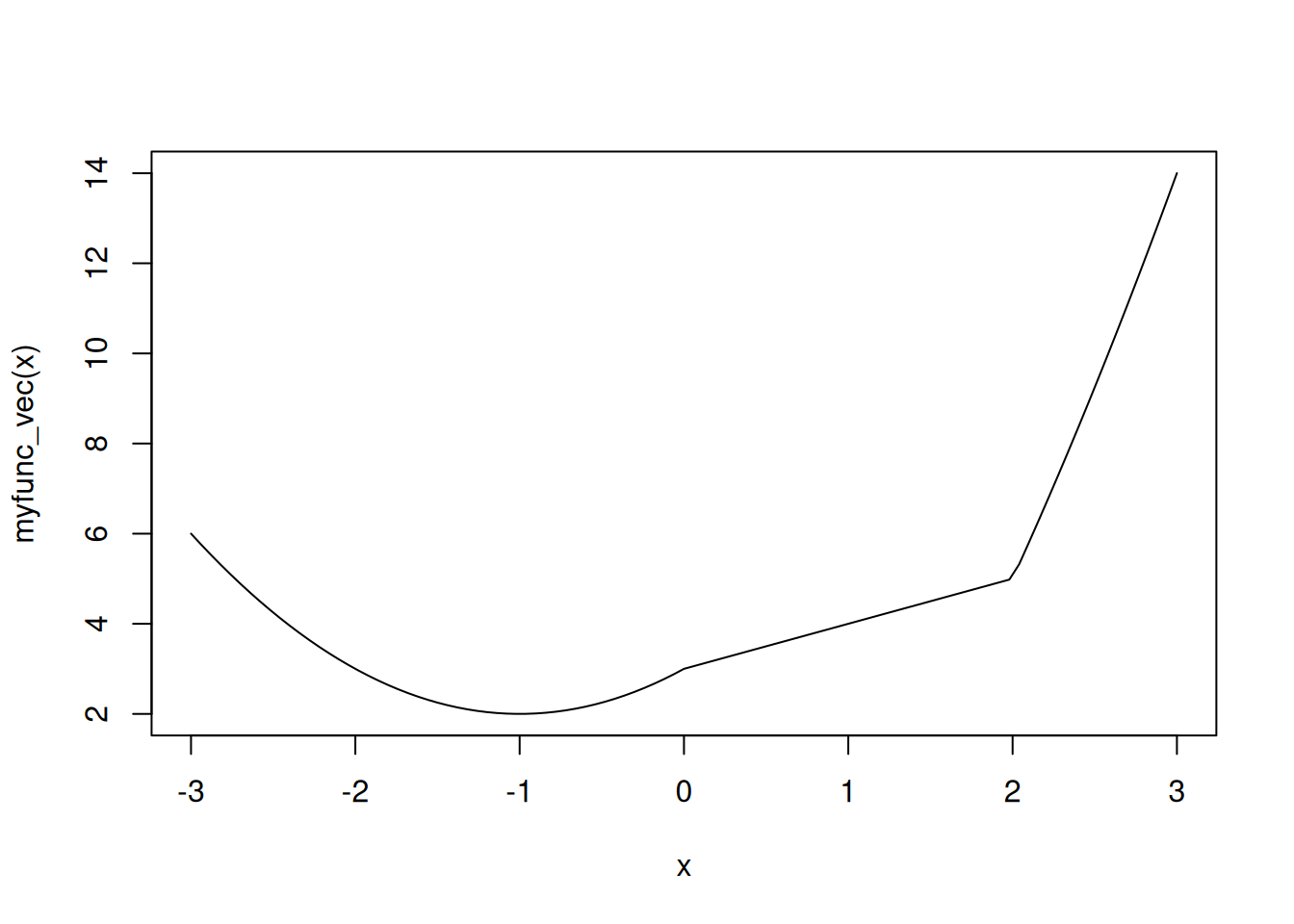
The same can also be achieved by wrapping sapply around the function defined in (a).
plot(x, sapply(x,myfunc), type="l")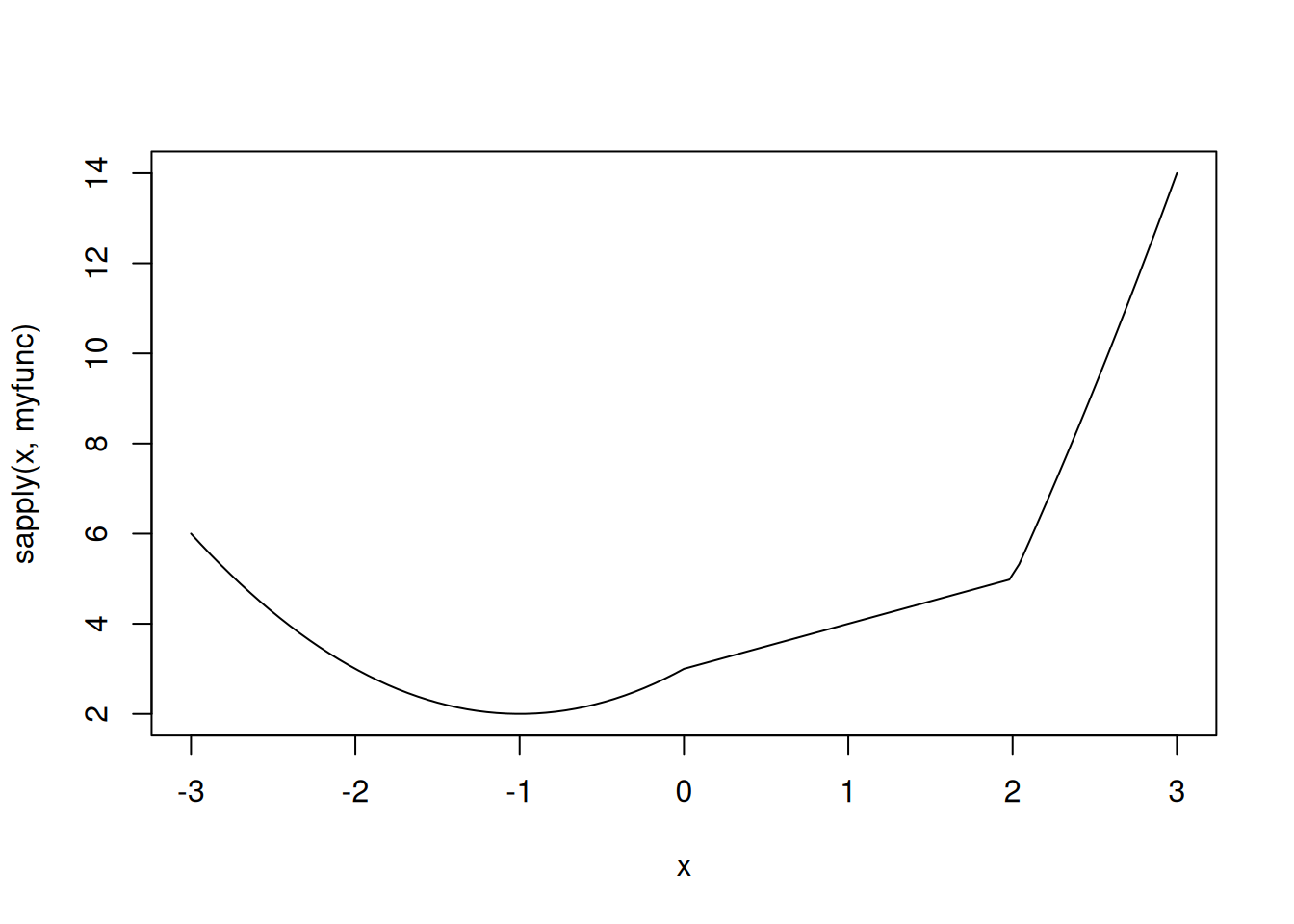
A particular homework is graded with A, B, C, or D according to the following scheme:
| Grade | Score |
|---|---|
| A | 81-100 |
| B | 61-80 |
| C | 41-60 |
| D | 0-40 |
Write an R program that reads the score from the user and prints the corresponding grade.
A bank has a variable interest rate depending on the account balance. The interest rate is 20% for balances less than 10,000 TL, 22% for balances up to 100,000 TL, and 25% for higher balances.
Write a function named interest that takes the current balance as its parameter, and returns the interest due according to this scheme.
x holds a random number between -1 and 1, drawn from a uniform distribution.x is positive, the variable y holds a random number drawn from a normal distribution with mean 0 and standard deviation 1.x is zero or negative, the variable y holds a random number drawn from a normal distribution with mean 1 and standard deviation 0.5.x holds a vector of 100 random numbers between -1 and 1, drawn from a uniform distribution.y holds 100 random numbers depending on elements in x according to the rule given in part (a).